21-NSIJ2ME2 : Corrigé⚓︎

Année : 2021
Centre : Métropole candidats libres
Jour : 2
Enoncé :

Exercice 1⚓︎

bases de données relationnelles et langage SQL

On insère deux entrées dans lesquelles l'attribut idEleve est égal à 128. Or cet attribut est la clé primaire de la table, il ne peut pas exister en doublon.
Il s'agit de la clé étrangère idEleve qui doit respecter la contrainte d'intégrité référentielle.

🗂️ Requête SQL

SELECT titre
FROM Livres
WHERE auteur = 'Molière'

On compte les élèves de la table Eleves dont la classe est la 'T2'.

5.

🗂️ Requête SQL

UPDATE Emprunts
SET dateRetour = '2020-09-30'
WHERE idEmprunt = 640

On récupère les noms et prénoms des élèves de la classe 'T2' qui ont déjà emprunté un livre.
On propose (en utilisant l'ISBN cité dans la question 5):

🗂️ Requête SQL

SELECT nom, prenom
FROM Eleves
JOIN Emprunts ON Eleves.idEleves = Emprunts.idEleves
WHERE Emprunts.isbn = 192

Sans l'ISBN :

🗂️ Requête SQL

SELECT nom, prenom
FROM Eleves
JOIN Emprunts ON Eleves.idEleves = Emprunts.idEleves
JOIN Livres ON Livres.isbn = Emprunts.isbn
WHERE Livres.titre = 'Les Misérables'

Exercice 2⚓︎

gestion des processus et des ressources par un système d'exploitation

1.a Un processus élu est en cours d'exécution par le processeur actuellement.

1.b.

flowchart LR
    A(prêt) --> B(élu)
    B --> A
    B --> C(bloqué)
    C --> A
    B ---> D(terminé)

2.a La file correspond au paradigme " Premier entré, premier sorti ".

2.b.

📋 Texte

![Frise complétée](data/images-21-ME2-ex2/ex2.svg)

3.a. Il s'agit d'un problème d'interblocage car les deux processus verrouillent simultanément les fichiers 1 et 2.

3.b. On échange simplement les deux premières lignes du programme 2 :

📋 Texte

| Programme 1             | Programme 2             |
| :---------------------- | :---------------------- |
| Verrouiller fichier_1   | Verrouiller fichier_1   |
| Calculs sur fichier_1   | Verrouiller fichier_2   |
| Verrouiller fichier_2   | Calculs sur fichier_1   |
| Calculs sur fichier_1   | Calculs sur fichier_2   |
| Calculs sur fichier_2   | Déverrouiller fichier_1 |
| Calculs sur fichier_1   | Déverrouiller fichier_2 |
| Déverrouiller fichier_2 |                         |
| Déverrouiller fichier_1 |                         |

Exercice 3⚓︎

arbres binaires de recherche et programmation orientée objet

1.a. La taille de l'arbre est 7.

1.b. La hauteur de l'arbre est 4.

2

graph TD
    A(10) --> B(5) 
    B --> D(4)
    B --> E(8)
    A --> C(15)
    C --> F(12)
    C --> G(20)

3

graph TD
    A(10) --> B(8) 
    B --> D(4)
    D --> D1(" ")
    D --> D2(5)
    B --> E(" " )
    E --> E1(" ")
    E --> E2(" ")
    A --> C(20)
    C --> F(15)
    C --> G(" ")
    F --> H(12)
    F --> J(" ")
    G --> G1(" ")
    G --> G2(" ")
    linkStyle 2 stroke-width:0px;
    style D1 opacity:0;
    linkStyle 4 stroke-width:0px;
    style E opacity:0;
    linkStyle 5 stroke-width:0px;
    style E opacity:0;
    linkStyle 6 stroke-width:0px;
    style E1 opacity:0;
    style E2 opacity:0;
    linkStyle 9 stroke-width:0px;
    style G opacity:0;
    linkStyle 11 stroke-width:0px;
    style J opacity:0;
    linkStyle 12 stroke-width:0px;
    style G1 opacity:0;
    linkStyle 13 stroke-width:0px;
    style G2 opacity:0;

4.

🐍 Script Python
def hauteur(self):
    return self.racine.hauteur()

5. Méthode taille de la classe Noeud :

🐍 Script Python
def taille(self):
    if self.gauche is None and self.droit is None:
        return 1
    elif self.gauche is None:
        return 1 + self.droit.taille()
    elif self.droit is None:
        return 1 + self.gauche.taille()
    else:
        return 1 + self.gauche.taille() + self.droit.taille()

Méthode taille de la classe Arbre :

🐍 Script Python
def taille(self):
    return self.racine.taille()

6.a. La configuration minimale d'un arbre bien construit de hauteur \(h\) peut être :

📋 Texte

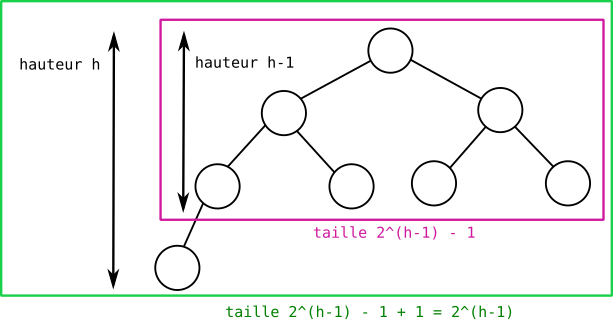![image](data/ex3-6a.png){: .center}

La taille minimale ```min``` est donc égale à $2^{h-1}$.

6.b. Intuitivement, un arbre est mal construit si sa hauteur est trop grande par rapport à sa taille (trop étiré).

Donc un arbre est mal construit si sa taille est trop petite par rapport à sa hauteur.

Donc un arbre de taille \(t\) et de hauteur \(h\) est mal construit si \(t < 2^{h-1}\), puisqu'on a démontré que \(2^{h-1}\) était la taille minimale.

Pour tester si un arbre est bien construit, on va donc juste vérifier que \(t \geqslant 2^{h-1}\) :

🐍 Script Python
def bien_construit(self):
    h = self.taille()
    return self.taille() >= 2**(h-1)

Exercice 4⚓︎

programmation et récursivité

Exercice 5⚓︎

programmation

a Si les éléments du tableau sont tous positifs, il suffit d’additionner tous les éléments du tableau pour obtenir la somme maximale (la sous-séquence correspond à l’ensemble du tableau).

b. Si les éléments du tableau sont tous négatifs, il suffit de prendre l’élément le plus grand du tableau (la sous-séquence est réduite à un seul élément)

a

🐍 Script Python

def somme_sous_sequence(lst, i, j):
    somme = 0
    for ind in range(i,j+1):
        somme = somme + lst[ind]
    return somme

b. Pour un tableau de 10 éléments, nous avons 55 comparaisons \((10+9+8+7+6+5+4+3+2+1=55)\).

c.

🐍 Script Python

def pgsp(lst):
    n = len(lst)
    somme_max = lst[0]
    i_max = 0
    j_max = 0
    for i in range(n):
        for j in range(i,n):
            s = somme_sous_sequence(lst,i,j)
            if s > somme_max:
                somme_max = s
                i_max = i
                j_max = j
    return (somme_max, i_max, j_max)

a.

b.

🐍 Script Python

def pgsp2(lst):
    somme_max = [lst[0]]
    for i in range (1,len(lst)):
        if somme_max[i-1] <= 0:
            somme_max.append(lst[i])
        else :
            somme_max.append(lst[i]+somme_max[i-1])
    return max(somme_max)

c. Cette solution est plus avantageuse, car la complexité en temps de l’algorithme est en \(O(n)\) alors que dans le cas précédent il était en \(O(n^2)\).